LU-SGS versus DPLUR

Comparison of Implicit Methods Available In Aither

Aither v0.3.0 contains four implicit methods for solving the system of equations selected. Lower-Upper Symmetric Gauss Seidel (LU-SGS) [1], Block Lower-Upper Symmetric Gauss Seidel (BLU-SGS) [2], Data Parallel Lower Upper Relaxation (DPLUR) [3], and Block Data Parallel Lower Upper Relaxation (BDPLUR) [4]. These four methods are similar in nature but have different performance characteristics depending on the problem at hand. At their core they all involve solving a system of equations. We start with the implicit discretization cast in delta form as shown below where $\Delta X^n = X^{n+1} - X^n$.

$$\frac{V}{\Delta t} \Delta W^n + = -R^{n+1}$$ $$R^{n+1} = R^n + \frac{\partial R^n}{\partial W^n} \Delta W^n + ...$$ $$\frac{V}{\Delta t} \left[ \frac{\partial R^n}{\partial W^n} \right] \Delta W^n = -R^n$$

In the above equation $\frac{\partial R^n}{\partial W^n}$ is a $N$ x $N$ block matrix where each block is $n$ x $n$. $N$ is the number of cells in the domain and $n$ is the number of equations being solved in each cell. $\Delta W^n$ and $-R^n$ are $N$ x 1 block vectors where each block is of size $n$ x 1. As you can see solving the Navier-Stokes equations implicitly boils down to solving the cannonical linear algebra problem $A x = b$. All four of the implicit methods within Aither start from this discretization. They differ only in the approximations made in constructing the matrix $A$, and the solution method. All four methods approximately solve $A x = b$, where LU-SGS and BLU-SGS use the Gauss Seidel method and DPLUR and BDPLUR use the Jacobi method. Since $A x = b$ is being solved approximately, there is no reason to waste computational expense to accurately calculate $A$. Since $A$ is being approximately calculated it is factored into lower trianguler, diagonal, and upper trianguler matrices.

$$A \approx L + D + U$$

All of the methods make varying approximations in constructing the implicit matrix. The LU-SGS and DPLUR methods approximate the $L$, $D$, and $U$ matricies with their spectral radii, while the BLU-SGS and BDPLUR methods use the full $n$ x $n$ matrix on the diagonal. The approximations made by LU-SGS and DPLUR allow them to use less memory as they do not need to store a full matrix for $D$, but only a scalar value. They are also more computationally efficient as the inversion of the $D$ matrix is trivial. The BLU-SGS and DPLUR methods make less approximations and therefore should converge in fewer iterations. However, they are more computationally expensive and require more memory. Using the full matrix on the diagonal hurts the diagonal dominance of the linear system making these methods less stable. They may require a lower CFL number than their scalar diagonal counterparts.

Supersonic Wedge

To compare these implicit methods the simulation of supersonic turbulent flow over a 15 degree wedge was used. Freestream conditions of 23842.3 $Pa$, 0.379597 $\frac{kg}{m^3}$, and 739.9 $\frac{m}{s}$ were used. The Reynolds-Averaged Navier-Stokes equations were solved with the Wilcox $k-\omega$ 2006 turbulence model. The block matrix methods became unstable when the default freetream eddy viscosity ratio of ten was used, so for these simulations all methods used 0.001. The grid used was 101 x 121 x 2 with near wall spacing of $1.0e^{-6} m$ to ensure a $y^+$ value less than one. The simulations were solved with second order accuracy in space using MUSCL reconstruction with Aither’s thirdOrder option. The minmod limiter was used to avoid spurious oscillations near the shock. Contours of Mach number and turbulent eddy viscosity are shown below.

Mach contour of supersonic flow over wedge.

Turbulent eddy viscosity ratio contour of supersonic flow over wedge.

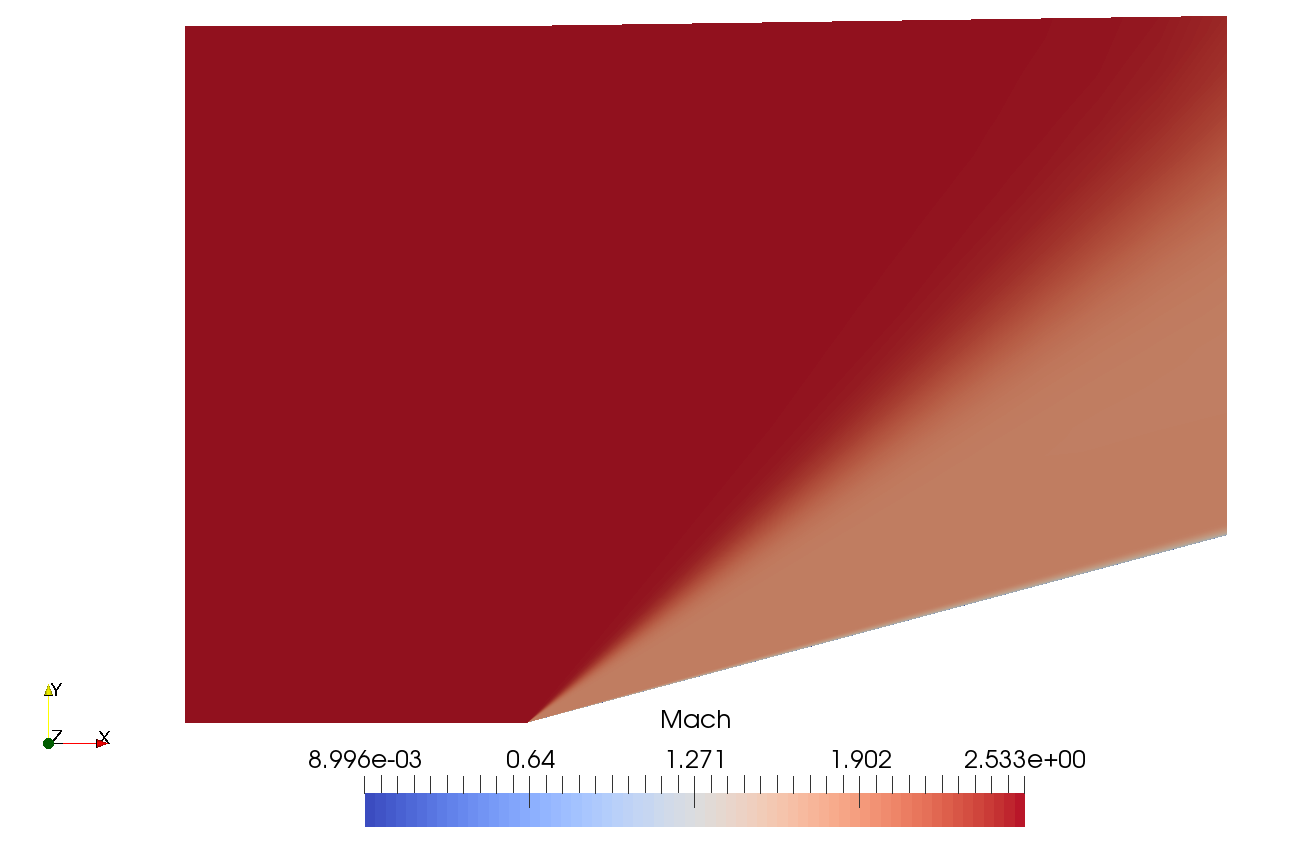
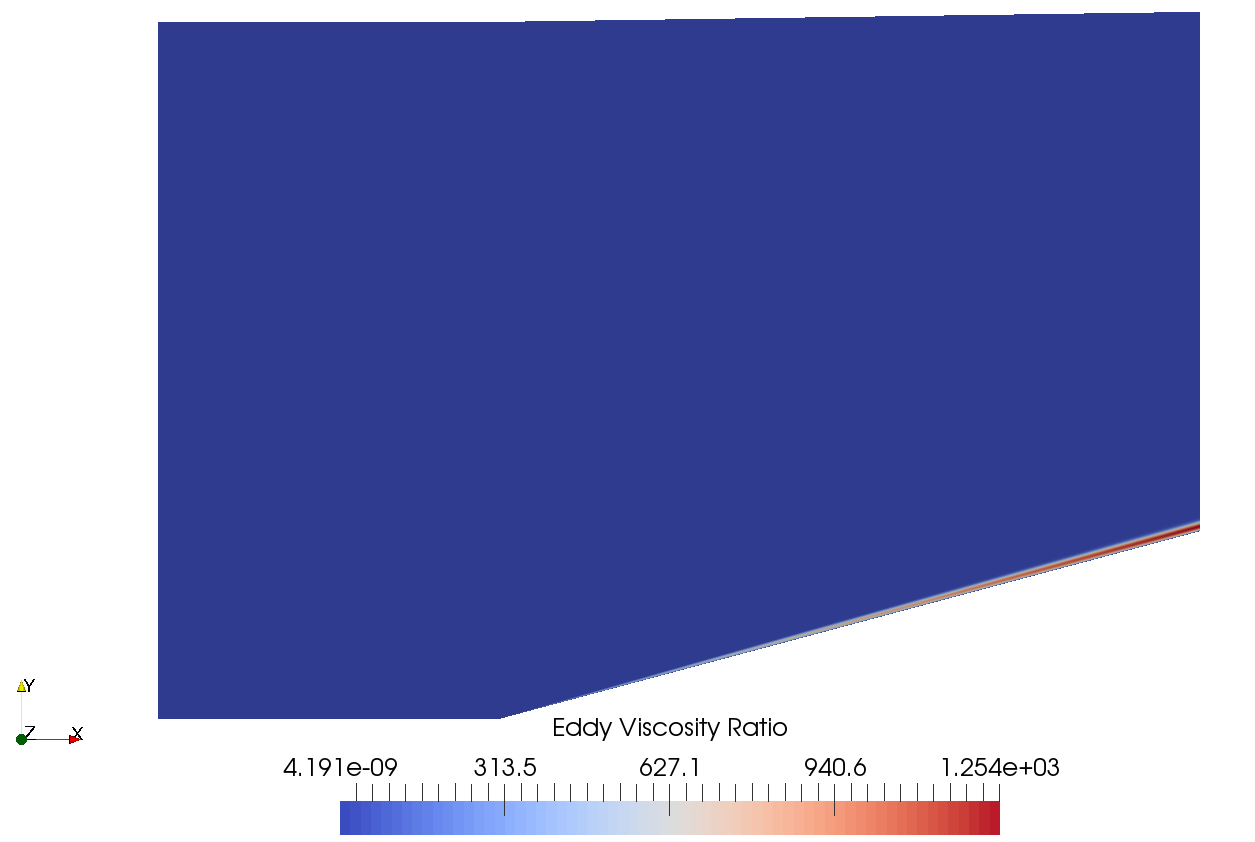
Implementation Of Implicit Methods

The implicit methods differ primarily in their construction of the $D$, $L$, and $U$ matrices. Since the $L$ and $U$ matrices are constructed in a similar was as the $D$ matrix, only the $D$ matrix will be shown here. The LU-SGS and DPLUR methods use an identical $D$ matrix. The BLU-SGS and BDPLUR methods use an indentical $D$ matrix as well. In all methods the $D$ matrix is the only one that is stored, while the $L$ and $U$ matrices are calculated on-the-fly. The mean flow and turbulence equations are handled separately, so two scalars are used for $D$ in the LU-SGS and DPLUR methods. For BLU-SGS and BDPLUR a 5 x 5 matrix and a 2 x 2 matrix (for a two equation turbulence model) are used. The inviscid flow jacobian follows the derivation in Blazek, and the viscous flow jacobian uses the thin shear layer approximation and the derivation shown in Dwight. The following definitions are used in the equations below: $\phi = 0.5 \left( \gamma - 1 \right) \vec{v} \cdot \vec{v}$, $v_n = \vec{v} \cdot \vec{n}$, $a_1 = \gamma E - \phi$, and $a_3 = \gamma - 2$

$$D_{scalar} = \lambda_i + \lambda_v + \lambda_s$$ $$\begin{equation} \lambda_{i_{flow}} = 0.5 A \left(\left| \vec{v} \cdot \vec{n} \right| + a \right) \qquad \lambda_{i_{turb}} = 0.5 A \left(\left| \vec{v} \cdot \vec{n} \right| + \vec{v} \cdot \vec{n} \right) \end{equation}$$ $$\begin{equation} \lambda_{v_{flow}} = \frac{A}{\Delta x} \left( \frac{\mu}{Pr} + \frac{\mu_t}{Pr_t} \right) max\left( \frac{4}{3 \rho}, \frac{\gamma}{\rho}\right) \qquad \lambda_{v_{turb}} = \frac{A}{\Delta x} \frac {\mu + \sigma_k \mu_t}{\rho} \end{equation}$$ $$\begin{equation} \lambda_{s_{flow}} = 0 \qquad \lambda_{s_{turb}} = -2 \beta^* \omega V \end{equation}$$

---

$$D_{block} = \frac{\partial F_i}{\partial W} - \frac{\partial F_v}{\partial W} - \frac{\partial S}{\partial W}$$ $$\frac{\partial F_{i_{flow}}}{\partial W} = \left[ \begin{array}{ccccc} 0 & n_x & n_y & n_z & 0 \\ \phi n_x - v_x v_n & v_n - a_3 n_x v_x & v_x n_y - \left(\gamma - 1 \right) v_y n_x & v_x n_z - \left(\gamma - 1 \right) v_z n_x & \left(\gamma - 1 \right) n_x \\ \phi n_y - v_y v_n & v_y n_x - \left(\gamma - 1 \right) v_x n_y & v_n - a_3 n_y v_y & v_y n_z - \left(\gamma - 1 \right) v_z n_y & \left(\gamma - 1 \right) n_y \\ \phi n_z - v_z v_n & v_z n_x - \left(\gamma - 1 \right) v_x n_z & v_z n_y - \left(\gamma - 1 \right) v_y n_z & v_n - a_3 n_z v_z & \left(\gamma - 1 \right) n_z \\ v_n \left(\phi - a_1 \right) & a_1 n_x - \left(\gamma - 1 \right) v_x v_n & a_1 n_y - \left(\gamma - 1 \right) v_y v_n & a_1 n_z - \left(\gamma - 1 \right) v_z v_n & \gamma v_n \end{array} \right]$$ $$\frac{\partial F_{i_{turb}}}{\partial W} = \left[ \begin{array}{cc} 0.5 A \left(\left| \vec{v} \cdot \vec{n} \right| + \vec{v} \cdot \vec{n} \right) & 0 \\ 0 & 0.5 A \left(\left| \vec{v} \cdot \vec{n} \right| + \vec{v} \cdot \vec{n} \right) \end{array} \right]$$ $$\frac{\partial F_{v_{flow}}}{\partial W} = \mp \frac{A \left(\mu + \mu_t \right)}{\Delta x} \left[ \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{3} n^2_x + 1 & \frac{1}{3} n_y n_x & \frac{1}{3} n_z n_x & 0 \\ 0 & \frac{1}{3} n_x n_y & \frac{1}{3} n^2_y + 1 & \frac{1}{3} n_z n_y & 0 \\ 0 & \frac{1}{3} n_x n_z & \frac{1}{3} n_y n_z & \frac{1}{3} n^2_z + 1 & 0 \\ \psi^{\pm}_{\rho} & \mp \frac{\Delta x}{2 \left(\mu + \mu_t\right)} n_l \tau_{lx}+ \pi_x & \mp \frac{\Delta x}{2 \left(\mu + \mu_t\right)} n_l \tau_{ly}+ \pi_y & \mp \frac{\Delta x}{2 \left(\mu + \mu_t\right)} n_l \tau_{lz}+ \pi_z & \psi^{\pm}_{p} \end{array} \right] \cdot \left[ \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ -\frac{v_x}{\rho} & \frac{1}{\rho} & 0 & 0 & 0 \\ -\frac{v_y}{\rho} & 0 & \frac{1}{\rho} & 0 & 0 \\ -\frac{v_z}{\rho} & 0 & 0 & \frac{1}{\rho} & 0 \\ \phi & -\left( \gamma - 1\right) v_x & -\left( \gamma - 1\right) v_y & -\left( \gamma - 1\right) v_z & \gamma - 1 \end{array} \right]$$ $$\begin{equation} \psi^+_{\rho} = -\frac{\left(\kappa + \kappa_t \right) T_l}{\left(\mu + \mu_t \right) \rho_l} \qquad \psi^-_{\rho} = -\frac{\left(\kappa + \kappa_t \right) T_r}{\left(\mu + \mu_t \right) \rho_r} \qquad \psi^+_{p} = -\frac{\left(\kappa + \kappa_t \right)}{\left(\mu + \mu_t \right) \rho_l} \qquad \psi^-_{p} = -\frac{\left(\kappa + \kappa_t \right)}{\left(\mu + \mu_t \right) \rho_r} \end{equation}$$ $$\begin{equation} \pi_x = \left(\frac{1}{3} n^2_x + 1\right) v_x + \frac{1}{3} n_y n_x v_y + \frac{1}{3} n_x n_x v_z \qquad \pi_y = \frac{1}{3} n_x n_y v_x + \left(\frac{1}{3} n^2_y + 1\right) v_y + \frac{1}{3} n_z n_y v_z \qquad \pi_z = \frac{1}{3} n_x n_z v_x + \frac{1}{3} n_y n_z v_y + \left(\frac{1}{3} n^2_z + 1\right) v_z \end{equation}$$ $$\frac{\partial F_{v_{turb}}}{\partial W} = \left[ \begin{array}{cc} \frac{A}{\Delta x} \frac{\mu + \sigma_k \mu_t}{\rho} & 0 \\ 0 & \frac{A}{\Delta x} \frac{\mu + \sigma_{\omega} \mu_t}{\rho} \end{array} \right]$$ $$\begin{equation} \frac{\partial S_{flow}}{\partial W} = 0 \qquad \frac{\partial S_{turb}}{\partial W} = \left[ \begin{array}{cc} -2 \beta^* \omega V & 0 \\ 0 & -2 \beta \omega V \end{array} \right] \end{equation}$$

Once the $D$ matrix is calulated and stored, the off-diagonal $L$ and $U$ matrices are computed on-the-fly during the matrix relaxation procedure. For the scalar methods the off diagonal is further approximated as shown below. For the block methods, the full matrix-vector multiplication is done on the off diagonals.

$$0.5 \left( \frac{\partial F}{\partial W} \Delta W A + \lambda \right) \approx 0.5 \left( \Delta F + \lambda\right)$$

Results

The four implicit methods were used to solve the supersonic wedge varying the number of sweeps (Gauss Seidel or Jacobi). The simulations were run for 10,000 iterations in parallel on 4 processors. Aither was compiled with GCC 6.1 and OpenMPI 2.0.0 on Ubuntu 16.04. The processor used was a quad core Intel Core i7-4700MQ @ 2.4GHz. Each simulation was only run once, so this was not a rigorous timing study. The table below shows a summary of all the cases run including the final mass residual L2 norm relative to the highest mass residual within the first 5 iterations. The matrix relaxation used is also shown. All cases except the BLU-SGS and BDPLUR cases with the lowest number of sweeps used the default value of 1. Since the block matrix methods have worse diagonal dominance, relaxation is occassionally needed to aid stability. All simulations were run using local time stepping with a CFL number of 1e5.

Method	Sweeps	Relaxation	Final Mass Residual	Simulation Time (s)
LU-SGS	1	1	3.9302e-5	477.4
LU-SGS	2	1	2.1304e-6	612.8
LU-SGS	4	1	2.6281e-8	893.7
DPLUR	2	1	6.5039e-5	503.3
DPLUR	4	1	2.0773e-5	603.9
DPLUR	8	1	1.9359e-6	870
BLU-SGS	2	1.1	1.4966e-5	2013
BLU-SGS	4	1	3.3500e-6	3223
BDPLUR	4	1.2	4.2507e-5	2057
BDPLUR	8	1	1.6883e-5	3319

Convergence of the mass residual.

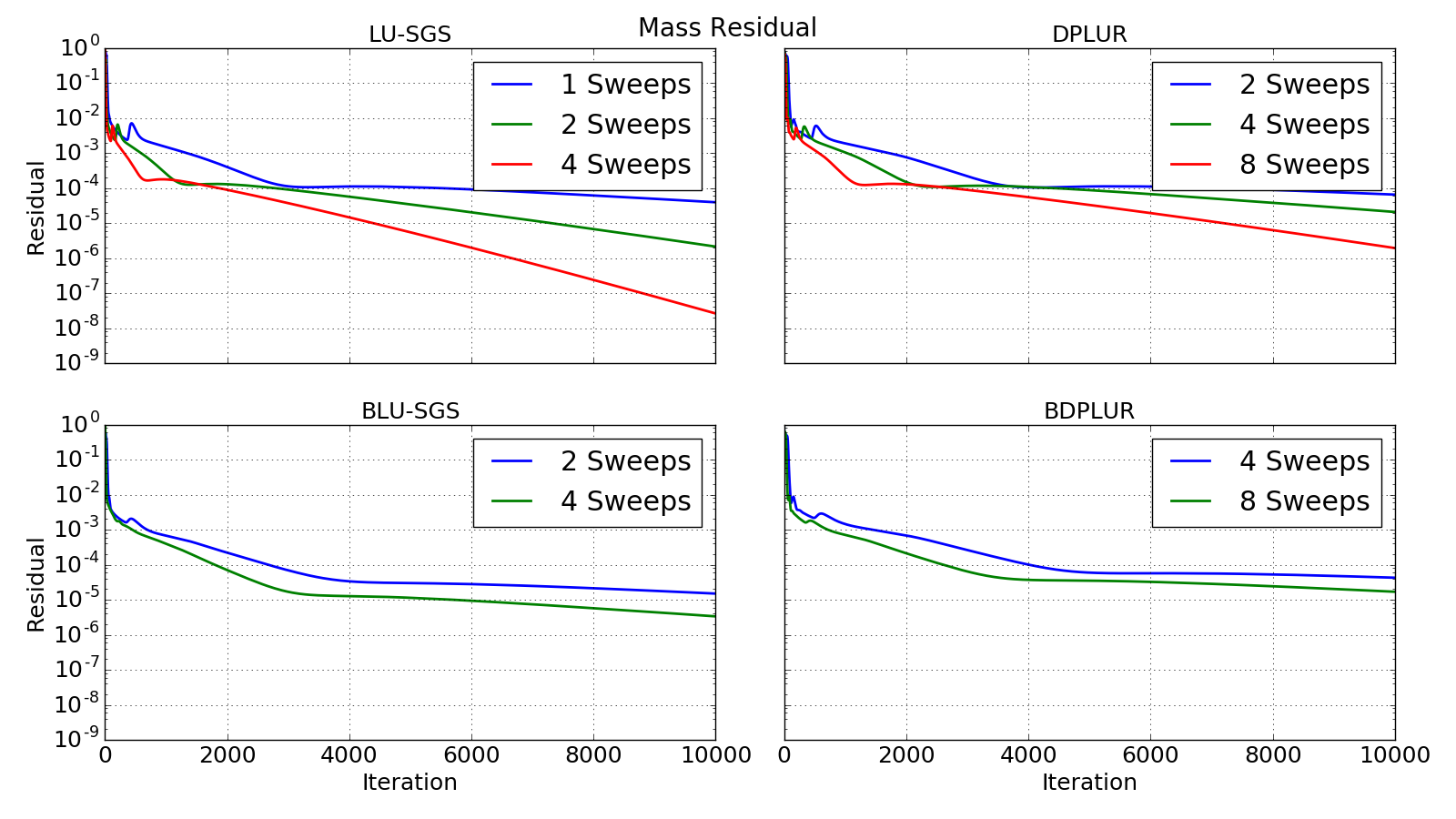
The same behavior is shown with the residuals for the other equations, so they are omitted here. The number of sweeps for the DPLUR based methods was doubled compared to their LU-SGS based counter parts because the DPLUR methods use a Jacobi relaxation instead of the 2x more efficient Gauss Seidel relaxation. It is expected that the block matrix based methods take longer due to the increase in computational effort required. However these methods will likely improve in later versions of Aither as a linear matrix library such as Eigen or PETSc is slated to be used. Based on the literature it is expected that the block matrix methods should perform better on highly stretched grids such as this one used for a RANS simulation. However, for this case the benefit of the block matrix methods is not observed. Previous simulations have shown a small benefit to using the block matrix methods in some cases, but usually not enough to justify their extra cost.

Conclusions

For the supersonic wedge case analyzed here, LU-SGS has the best performance. It is stable and efficient. The block matrix based methods show rather poor performance in terms of residual drop and simulation time, however the latter is expected to improve in future versions of Aither. For cases other than this one, the block matrix methods have shown better convergance than their scalar counterparts, and no need to increase the relaxation factor from the default value of 1. How do these results compare with your experience? Comment below!

References

[1] Yoon, S and Jameson, A. Lower-Upper Symmetric-Gauss-Seidel Method for the Euler and Navier-Stokes Equations. 1988. AIAA Journal Vol 26 No 9.

[2] Chen, R. F. and Wang, Z. J. Fast, Block Lower-Upper Symmetric Gauss-Seidel Scheme for Arbitrary Grids. December 2000. AIAA Journal Vol 38 No 12.

[3] Candler, G. V. et al. A Data-Parallel LU-SGS Method for Reacting Flows. 1994. AIAA 94-0410.

[4] Wright, M. J et al. Data-Parallel Lower-Upper Relaxation Method for the Navier-Stokes Equations. 1996. AIAA Journal Vol 34 No 7.