Sod's Shock Tube

Sod’s Shock Tube

Sod’s shock tube [1] is a 1D canonical problem used to test the accuracy of CFD codes. The problem consists of a fluid in a tube divided by a diaphragm. The fluid on the left side of the diaphragm is at a high pressure, and the fluid on the right side of the diaphragm is at a lower pressure. At time t = 0, the diaphragm is punctured and the fluid is allowed to mix. This results in a right moving shock wave and contact discontinuity, and a left moving expansion wave. Numerically this can be simulated by solving the Euler equations. The exact solution can be determined analytically and used to compare to the CFD simulation result. Anderson’s book [2] describes the process for computing the analytical solution.

Typically the flow variables are normalized by the high pressure state, so that the initial conditions of the simulation are as shown.

$$Q_l = \left[ \begin{array}{c} \rho_l \\ v_{x_l} \\ v_{y_l} \\ v_{z_l} \\ P_l \\ \end{array} \right] = \left[ \begin{array}{c} 1.0 \\ 0.0 \\ 0.0 \\ 0.0 \\ 1.0 \\ \end{array} \right] ; Q_r = \left[ \begin{array}{c} \rho_r \\ v_{x_r} \\ v_{y_r} \\ v_{z_r} \\ P_r \\ \end{array} \right] = \left[ \begin{array}{c} 0.125 \\ 0.0 \\ 0.0 \\ 0.0 \\ 0.1 \\ \end{array} \right]$$

Reconstruction Schemes

In the cell-centered finite volume method, the volume averaged flow variables are stored at the centroid of the cell. To calculate the fluxes at the cell faces, the flow variables are needed at the cell faces. The solution therefore must be reconstructed from the cell centroids to the cell faces. How this is done can greatly effect the accuracy of the simulation. The Sod’s shock tube problem was run using three of the reconstruction methods available in Aither: constant, thirdOrder (MUSCL), and weno.

Constant Reconstruction

Constant reconstruction is a zeroth order reconstruction that results in a first order accurate simulation. In this method the flow variables at the cell face are set equal to the flow variables at the adjacent cell center. While very robust, this method is quite dissipative. It typically results in a solution that is not accurate enough for engineering purposes, as important flow features such as shocks are smeared.

MUSCL Reconstruction

MUSCL schemes were originally developed by van Leer. The stencil for this family of schemes uses the flow variables at two cell centers upwind, and one downwind of the cell face. The MUSCL schemes vary the weights of the flow variables in the stencil via a parameter $\kappa$. For most values of $\kappa$ the scheme results in a piecewise linear reconstruction which in turn results in a second order accurate simulation. However, when $\kappa$ is set equal to one third, the scheme results in a piecewise parabolic reconstruction that is third order accurate. However, due to the assumption that the flux is constant over the cell face, the simulation is still second order accurate. The solution error for a simulation with $\kappa$ equal to a third will typically be lower than for other values of $\kappa$.

The MUSCL scheme by itself as with all higer order accurate schemes suffers from spurious oscillations around discontinuities. In practice the reconstruction is limited through the use of a slope limiter. This means that near discontinuities the order of accuracy of the reconstruction is dropped to avoid the spurious oscillations.

WENO Reconstruction

Weighted essentially non-oscillatory (WENO) schemes [3] were originally developed by Shu. The stencil for this family of schemes uses the flow variables at three cell centers upwind, and two downwind of the cell face. The WENO scheme uses the piecewise parabolic reconstruction of the MUSCL scheme with $\kappa$ equal to one third over three candidate substencils. The first of the three substencils consists of the three upwind cells. The second consists of two upwind cells and one downwind cell. The third substencil consists of one upwind cell and two downwind cells. These three substencils are then weighted and combined to produce a fifth order accurate reconstruction in smooth regions of the flow. In areas near discontinuties, the substencils containing discontinuities are weighted to not contribute to the reconstruction which drops the order of accuracy. Even though the reconstruction can be fifth order accurate, the simulation will still be limited to second order accuracy due to the assumption of a constant flux on the cell face.

Results

The results at nondimensionalized time t = 0.1 are shown below. Near the discontinuities, the excessive dissipation of the constant reconstruction can be seen. As expected, the MUSCL and WENO schemes do much better.

Shock tube results for constant, MUSCL, and WENO reconstructions.

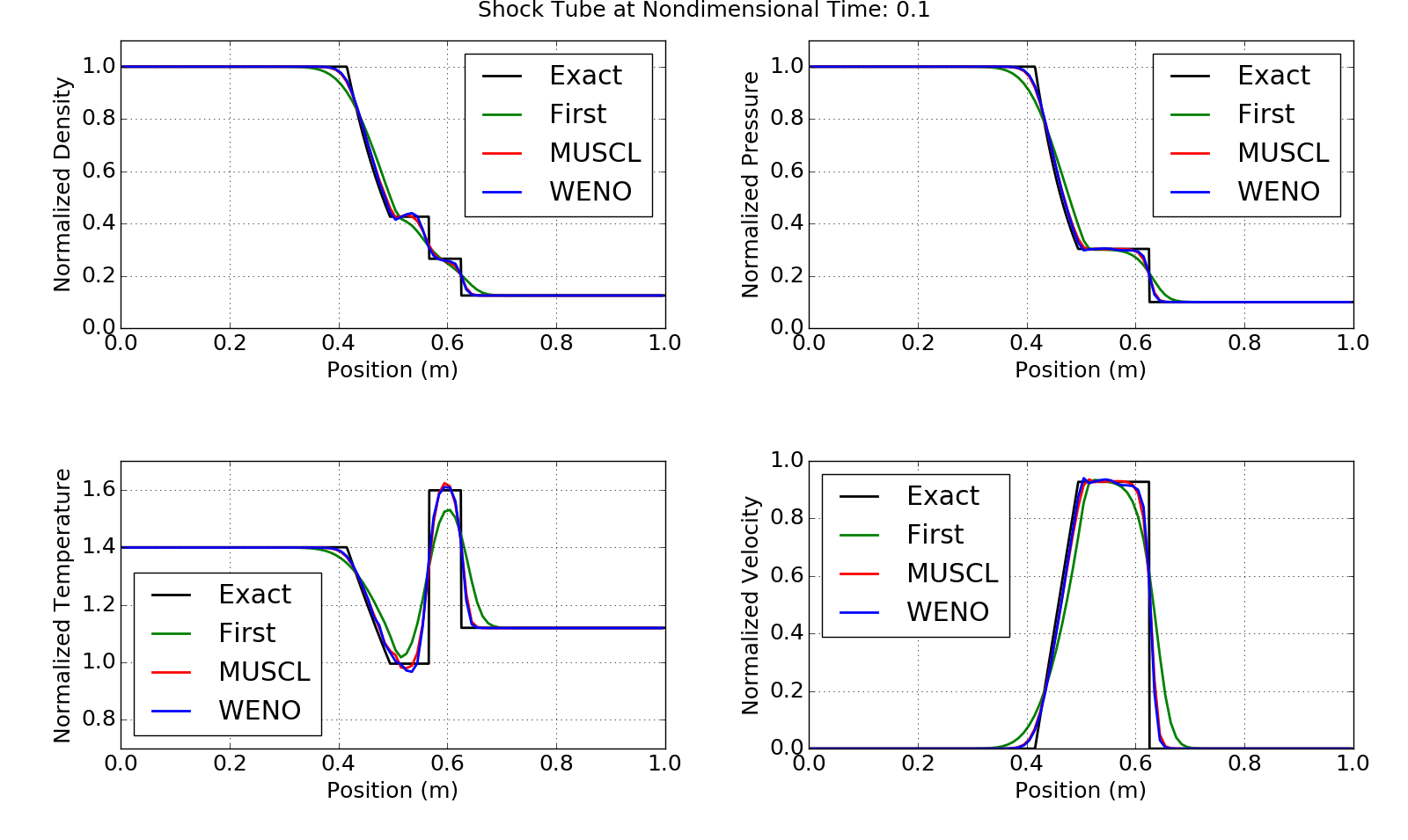
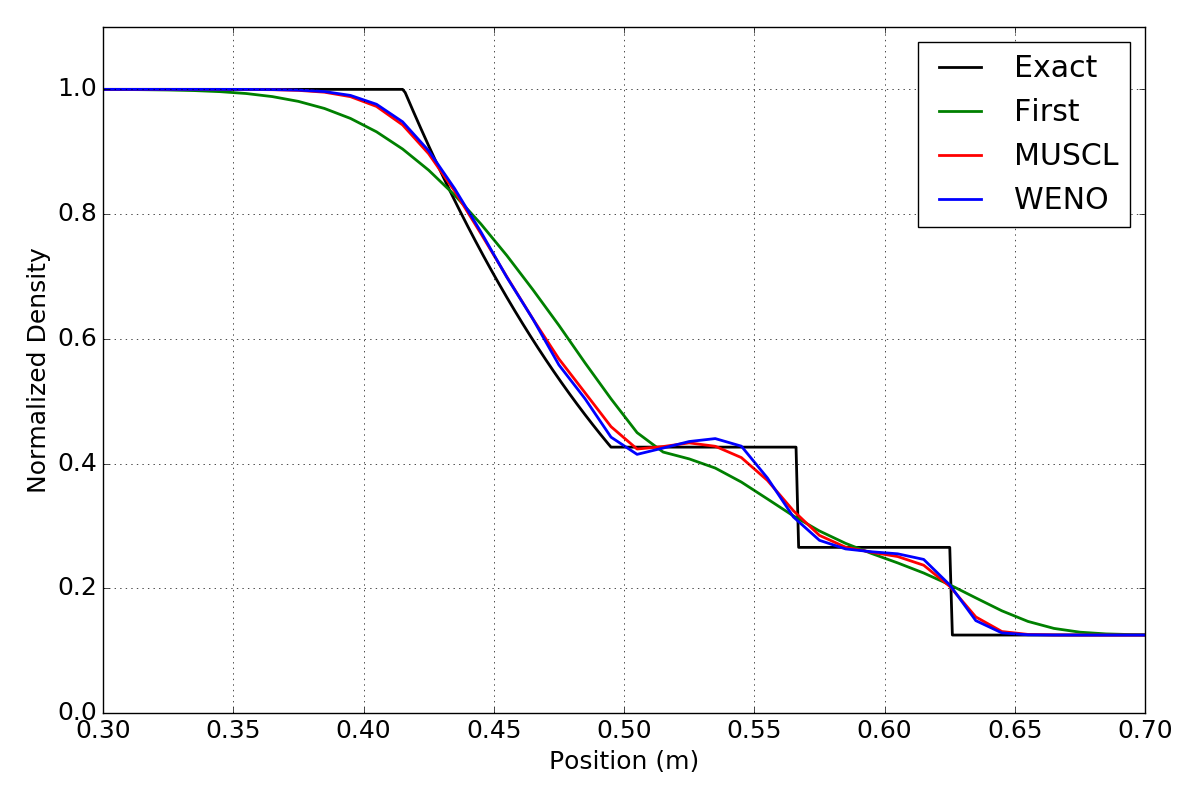
It is tough to tell the difference between the MUSCL and WENO results, so a zoomed in view of the normalized density is shown below. In the picture below is can be seen that the WENO scheme does slightly better in that it is a bit sharper near the discontinuities. This is due to its higher order accuracy in the reconstruction.

Detail view of density showing expansion, contact, and shock waves.

Summary

The WENO scheme provides the most accurate simulation of Sod’s shock tube problem. The constant reconstruction method provides the most dissipative solution. These results can be reproduced by running the Aither code. The grid and input file for the shock tube case can be found in the testCases directory of the repository. The python script used to compare the results to the exact simulation can be found here.

References

[1] Sod, G. A. “A Survey of Several Finite Difference Methods for Systems of Nonlinear Hyperbolic Conservation Laws”, Journal of Computational Physics, Vol 27, pp 1-31. 1978.

[2] Anderson, J. “Modern Compressible Flow with Historical Perspective”. McGraw-Hill Education, 2002.

[3] Shu, C. “Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws”. NASA CR-97-206253. ICASE Report No. 97-65. 1997.