Nonreflecting Outlet Boundary Condition

Subsonic Outflow

At a subsonic outflow there are four characteristics leaving the domain and one characteristic entering the domain. This means that the flow state on the boundary can be calculated from the interior cell’s state for four of the five primative variables. Typically density and the three components of velocity are calculated from the interior cell’s state. This leaves pressure to specified using other information supplied by the user. This user supplied data is used with the incoming characteristic to determine the pressure on the boundary. The incoming 1D characteristic equation, with characteristic variable $w$ is shown below.

$$\frac{\partial w}{\partial t} = \frac{\partial u}{\partial t} - \frac{1}{\rho c} \frac{\partial p}{\partial t}$$

Standard Pressure Outlet

With a standard pressure outlet, the implementation in most codes to to set the boundary pressure to a user defined value (shown below). This means that in the above characteristic equation $\frac{\partial p}{\partial t} = 0$ which shows that there is a reflection of intensity $\frac{\partial u}{\partial t}$. This reflection can delay convergence as well as corrupt simulations where acoustic pressure fluctuations are important. Some such simulations would be aeroacoustic simulations and/or large eddy simulations.

$$p_b = p_{ref}$$

Nonreflecting Outlet

For a truly nonreflecting outlet $\frac{\partial w}{\partial t} = 0$. However using this boundary condition can cause difficulty with setting the pressure on the boundary. When this boundary condition is used, the boundary pressure tends to float [1]. For this reason a relaxation coefficient $\kappa$ is typically used. Rudy and Strikwerda [2] suggested $\kappa$ in the form shown below where $M_{max}$ is the maximum Mach number on the boundary. The boundary condition proposed by Rudy and Strikwerda uses the locally one-dimensional inviscid (LODI) assumption. Many researchers have extended this approach to account for multi-dimensional flow at the outlet boundary by including the effect of transverse terms, $T$ [3]. The nonreflecting boundary condition is shown below where superscripts represent the time level of the variables.

$$p_{b}^{n+1} = \frac{ p^n + \rho^n c^n \left( \overrightarrow{v}^{n+1} - \overrightarrow{v}^{n} \right) \cdot \overrightarrow{n} + \Delta t \kappa p_{ref} - \Delta t \beta T} {1 + \Delta t \kappa}$$ $$\kappa = \frac{\sigma c^n \left( 1 - M_{max}^{2} \right)}{l}$$

The transverse terms are shown below. Here the subscript $t$ represents the transverse direction, and the subscript $n$ represents the boundary normal direction. For the $\beta$ calculation, the Mach number used is the average Mach number on the boundary.

$$\beta = M_{avg}$$ $$T = -0.5 \left[ \overrightarrow{v}_{t}^{n} \cdot \left( \overrightarrow{\nabla}_{t} p^n - \rho^n c^2 \overrightarrow{\nabla}_{t} \overrightarrow{v}_{n}^{n} \right) + \gamma p^n \overrightarrow{\nabla}_{t} \cdot \overrightarrow{v}_{t}^{n} \right]$$

Convecting Lamb-Oseen Vortex

A common test case for nonreflecting boundary conditions is a vortex convecting through an outlet boundary [1]. Ideally the vortex leaves the domain and there are no pressure waves reflected back into the domain. With a standard pressure outlet implementation, this will not be the case. Nonreflecting boundary conditions can significantly reduce the reflections at the boundary.

A test case was added to Aither for a convecting vortex corresponding to Case C in [1]. This simulation involves $N_2$ with a nominal pressure of 101300 Pascals and temperature of 288 Kelvin. The freestream flow is 100 meters per second with a Lamb-Oseen vortex with strength of 0.11 $\frac{m^2}{s}$ centered at the middle of the domain superimposed on the freestream flow. The radius of the vortex is one tenth the length of the domain. Results for the standard outlet and nonreflecting outlet are shown below in terms of the nondimensional pressure $p^{*}$. Note that the $p^{*}$ used in the plot is the opposite that used in [1]. This is because it is more intuitive that the vortex core be shown as having low pressure.

$$p^{*} = \left(p - p_{ref} \right) \frac{2 R^2}{\rho \Gamma^2}$$

Comparison of standard pressure outlet with nonreflecting pressure outlet.

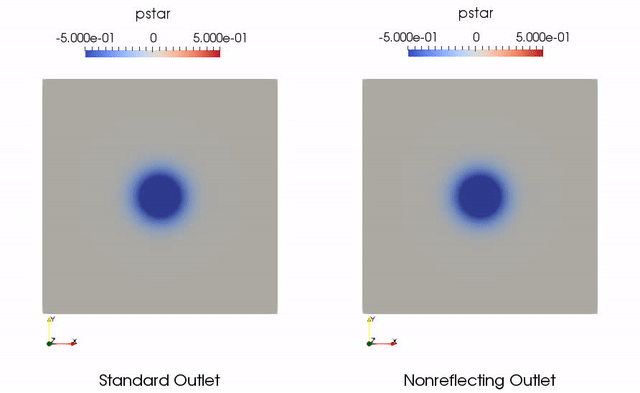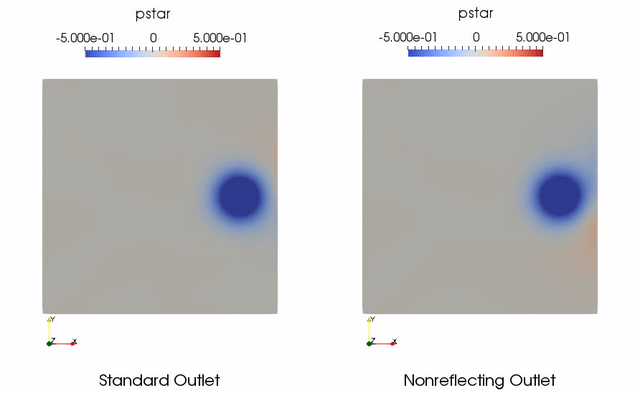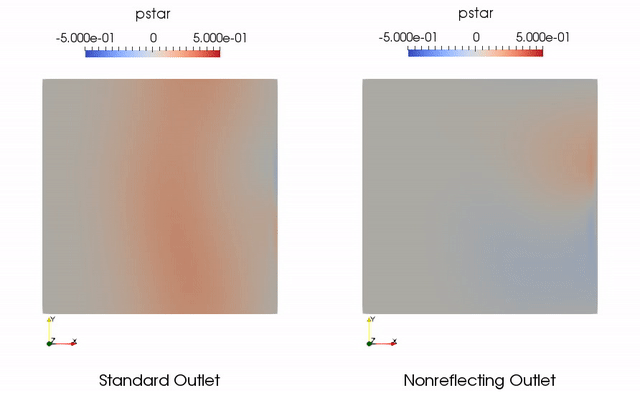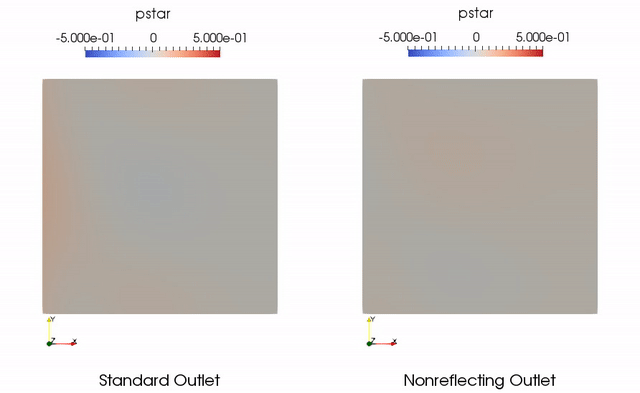
References

[1] Granet, Victor, et al. “Comparison of Nonreflecting Outlet Boundary Conditions for Compressible Solvers on Unstructured Grids”. 2010.

[2] Rudy, David and Strikwerda, John. “A Nonreflecting Outflow Boundary Condition for Subsonic Navier-Stokes Calculations”. Journal of Computational Physics. Vol 36, pp 55-70. 1980.

[3] Yoo, C. S. and Im, H. G. “Characteristic Boundary Conditions for Simulations of Compressible Reacting Flows with Multi-Dimensional, Viscous, and Reaction Effects”. June 29, 2006.