Dissociating Shock Tube
Problem Description
Version v0.9.0 of Aither added a finite rate reacting flow capability. To test this capability and to compare the effect of finite-rate chemistry to frozen chemistry and equilibrium chemistry, a test case for dissociating in a shock tube was added to the Aither testCases/dissociation directory. The simulation follows the description in Luke [1].
Initial Conditions
The shock tube is initialized with two separate flow states. The left side is initialized with a high temperature, high pressure, equilibrium mixture of and . Within this state there is already a significant amount of dissociation. The right state is intialized with a low temperature, low pressure, equilibrium mixture. This state has comparatively minimal dissociation. The flow states are shown below.
left: pressure=1e6 Pa, temperature=3000 K, mass fractions=[O2=0.9824, O=0.0176]
right: pressure=1e5 Pa, temperature=2000 K, mass fractions=[O2=0.9997, O=0.0003]
Chemistry Mechanisms
The shock tube simulation was run with three separate chemistry mechanisms for comparison. A frozen chemistry model, a finite-rate model, and an equilibrium model were used. Each of these models are present in Aither as of v0.9.0.
Frozen Chemistry
For the frozen chemistry simulation, no reactions were present. This is the default chemistry model for Aither. In can be explicitly selected by setting the chemistryModel to none or frozen in the input file as shown below.
chemistryModel: none
Finite-Rate Chemistry
The finite-rate reacting chemistry model can be selected by setting the chemistryModel to reacting in the input file. This simulation used a two species, two reaction chemistry mechanism (O2_2s2r) that comes with Aither. All chemistry mechanisms that come with Aither are installed to the ${AITHER_INSTALL_DIRECTORY}/chemistryMechanisms folder. This model and mechanism can be selected as shown below.
chemistryModel: reacting
chemistryMechanism: O2_2s2r
The chemistry mechanism is defined in Luke [1], but the rates have been converted to use instead of . The two reactions used in the mechanism are shown below.
2 O2 <=> 2 O + O2
O2 + O <=> 3 O
Equilibrium Chemistry
Aither doesn’t contain an explicit equilibrium chemistry model, but equilibrium chemistry can be simulated by increasing the reaction rates. The setup for the equilibrium chemistry simulation is identical to the the setup for the finite-rate simulation as shown below.
chemistryModel: reacting
chemistryMechanism: O2_2s2r
The reaction rates are increased by three orders of magnitude by copying the ${AITHER_INSTALL_DIRECTORY}/chemistryMechanisms/O2_2s2r.mch file into the run directory and increasing the C parameter in the Arrhenius fit by three orders of magnitude. Aither will first look for the mechanism file in the run directory before checking the installation directory, so this altered mechanism takes precedence over the version that comes with Aither.
Results
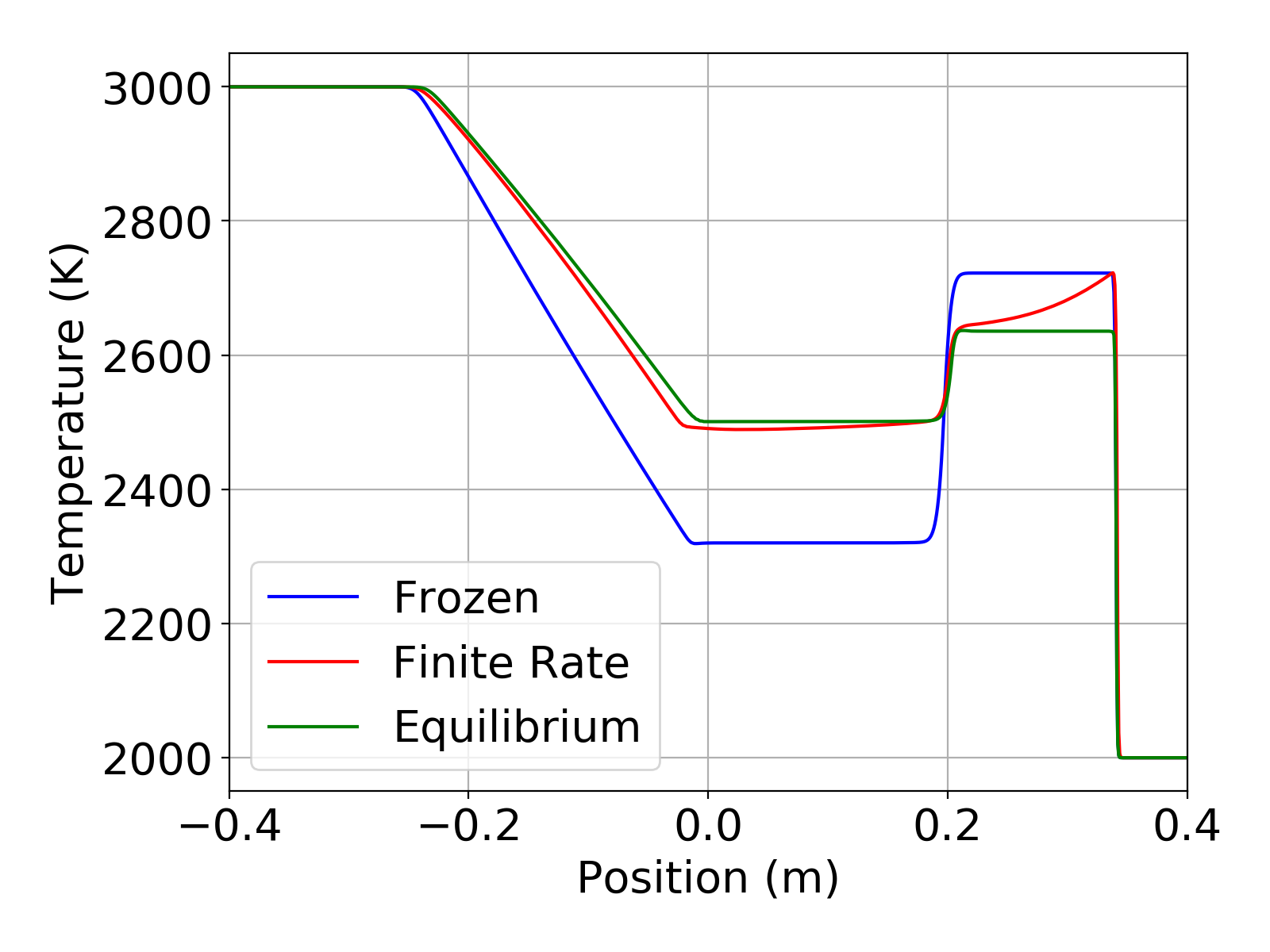
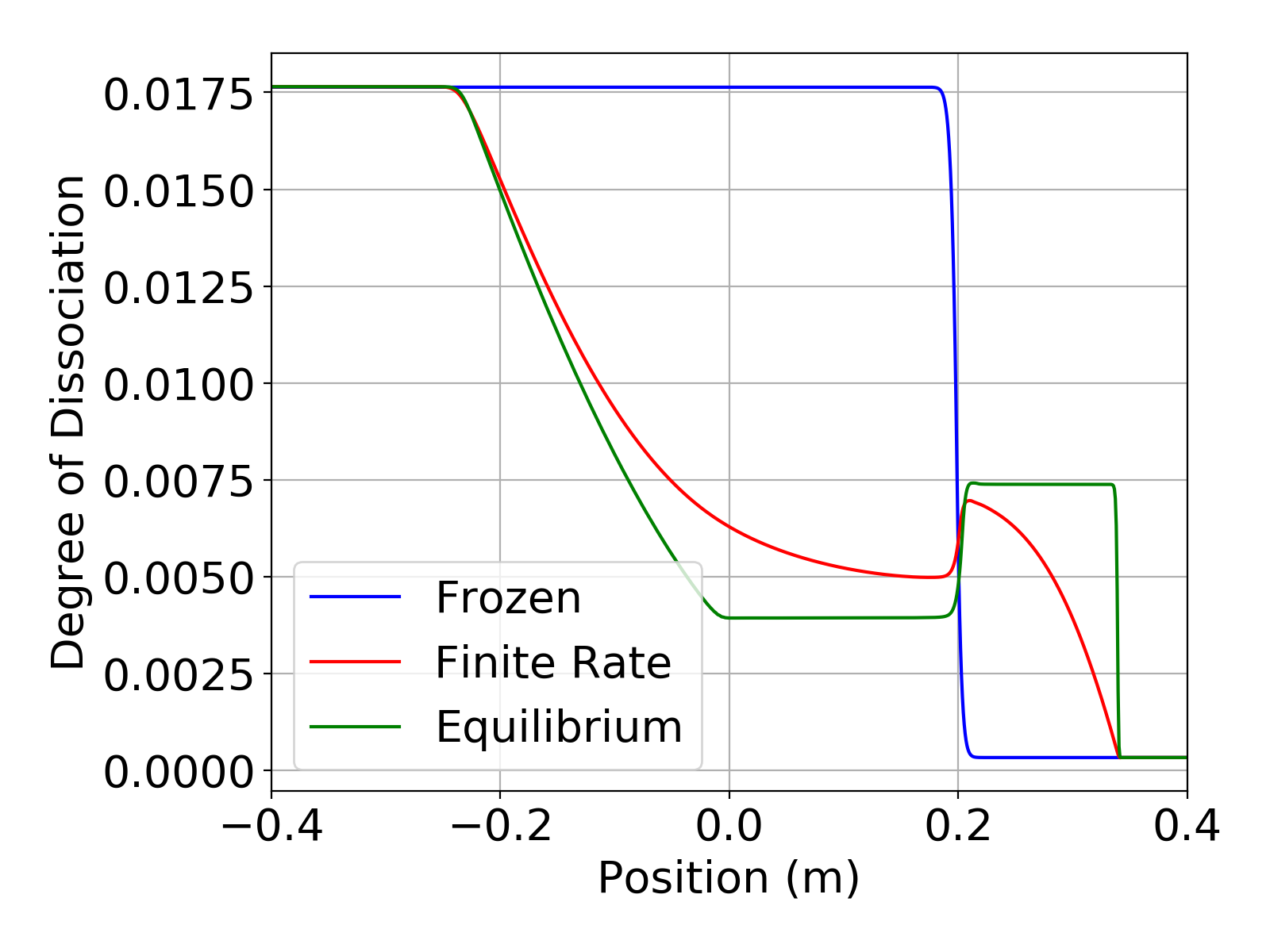
The simulations were run in a time accurate manner using a time step of 2e-7 seconds for a total time of 2.4e-4 seconds. The plots below show the temperature and degree of dissociation in the shock tube at the end of the simulation. For this simple mechanism the degree of dissociation is just the mass fraction of present. The temperature plot clearly shows the effect of finite-rate chemistry in the region behind the shock. The plots also show that the finite-rate solution is bounded by the frozen and equilibrium solutions. These results from Aither show excellent agreement with those in Luke [1].
References
[1] Luke, E. A. “A Rule-Based Specification System for Computational Fluid Dynamics”. Ph. D. Thesis. 1999.